Advertisements
Advertisements
प्रश्न
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
उत्तर
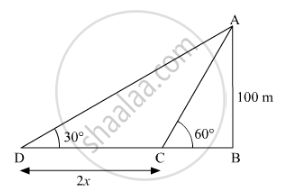
AB is a lighthouse of height 100m.
Let the speed of the boat be x metres per minute.
And CD is the distance which man travelled to change the angle of elevation.
So, CD = 2x ...[∵ Distance = Speed x Time]
tan (60°) = `("AB")/("BC")`
`sqrt(3) = (100)/("BC")`
⇒ `"BC" = (100)/(sqrt(3)`
tan (30°) = `("AB")/("BD")`
`(1)/sqrt(3) = (100)/("BD")`
`"BD" = 100 sqrt(3)`
`"CD"= "BD" - "BC"`
`2"x" = 100sqrt(3) - (100)/sqrt(3)`
`2"x" = (300-100)/sqrt(3)`
⇒ `"x" = (200)/(2sqrt(3)`
⇒ `"x" = (100)/(sqrt3)`
Using `sqrt(3)` = 1.73
`"x" = (100)/(1.73) ≈ 57.80`
Hence, the speed of the boat is 57.80">57.8057.80 metres per minute.
APPEARS IN
संबंधित प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
