Advertisements
Advertisements
प्रश्न
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
उत्तर
Let AC be the pedestal and BC be the statue such that BC = 1.46m.
We have:
∠ADC = 45° and ∠ADB = 60°
Let:
AC = hm and AD = xm
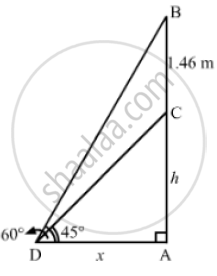
In the right ΔADC,we have:
`(AC)/(AD) = tan 45° = 1`
`⇒ h/x = 1`
⇒ h = x
Or,
x = h
Now, in the right ΔADB,we have:
`(AB)/(AD) = tan 60° = sqrt(3)`
`(h+1.46)/x = sqrt(3)`
On putting x = h in the above equation, we get
`(h+1.46)/h = sqrt(3)`
`⇒ h + 1.46 = sqrt(3)h`
`⇒ h( sqrt(3)-1) = 1.46`
`⇒ h = 1.46/( sqrt(3)-1) = 1.46/0.73 = 2m`
Hence, the height of the pedestal is 2 m.
APPEARS IN
संबंधित प्रश्न
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
In given figure, the value of ZC is ____________.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
