Advertisements
Advertisements
प्रश्न
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
उत्तर
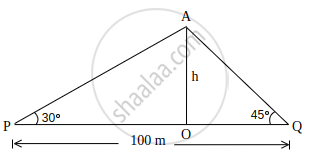
Let OA be the tree of height h m.
In ΔPOA, ∠O = 90°
tan 30° = `("OA")/("OP")`
⇒ `1/sqrt(3) = "h"/("OP")`
⇒ OP = `sqrt(3) "h"` ...(i)
In ΔQOA, ∠O = 90°
tan 45° = `("OA")/("OQ")`
⇒ `1 = "h"/("OQ")`
⇒ OQ = h ...(ii)
Adding equations (i) and (ii), we get
OP + OQ = `sqrt(3) "h" + "h"`
⇒ PQ = `"h"(sqrt(3) + 1)`
⇒ 100 = `"h"(sqrt(3) + 1)`
⇒ h = `100/(sqrt(3) + 1)`
⇒ h = `(100(sqrt(3) - 1))/((sqrt(3) + 1)(sqrt(3) - 1))`
⇒ h = `(100(sqrt(3) - 1))/2`
⇒ h = 50 (1.732 – 1)
⇒ h = 50 × 0.732
⇒ h = 36.6m
Thus, the height of the tree is 36.6 m.
संबंधित प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
