Advertisements
Advertisements
प्रश्न
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
उत्तर
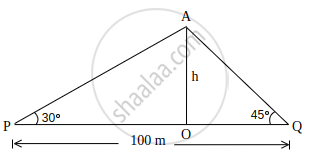
Let OA be the tree of height h m.
In ΔPOA, ∠O = 90°
tan 30° = `("OA")/("OP")`
⇒ `1/sqrt(3) = "h"/("OP")`
⇒ OP = `sqrt(3) "h"` ...(i)
In ΔQOA, ∠O = 90°
tan 45° = `("OA")/("OQ")`
⇒ `1 = "h"/("OQ")`
⇒ OQ = h ...(ii)
Adding equations (i) and (ii), we get
OP + OQ = `sqrt(3) "h" + "h"`
⇒ PQ = `"h"(sqrt(3) + 1)`
⇒ 100 = `"h"(sqrt(3) + 1)`
⇒ h = `100/(sqrt(3) + 1)`
⇒ h = `(100(sqrt(3) - 1))/((sqrt(3) + 1)(sqrt(3) - 1))`
⇒ h = `(100(sqrt(3) - 1))/2`
⇒ h = 50 (1.732 – 1)
⇒ h = 50 × 0.732
⇒ h = 36.6m
Thus, the height of the tree is 36.6 m.
संबंधित प्रश्न
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
The distance of point A(-5, 6) from the origin is ______.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]

