Advertisements
Advertisements
प्रश्न
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
उत्तर
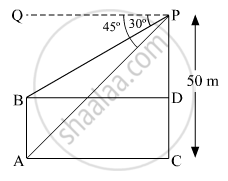
Let PC and AB represents the tower and the pole, respectively.
Suppose AB = x m.
From the above figure, we have
\[\angle PAC = \angle QPA = 45^o \left( \text{Alternate angles} \right)\]
\[\angle PBD = \angle QPB = 30^o \left( \text{Alternate angles} \right)\]
PD = PC − CD = PC − AB = (50 − x) m
In ∆PAC,
\[\tan45^o = \frac{PC}{AC}\]
\[ \Rightarrow 1 = \frac{PC}{AC}\]
\[ \Rightarrow AC = PC = 50 m\]
In ∆PBD,
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{PD}{BD}\]
\[ \Rightarrow BD = PD\sqrt{3}\]
\[ \Rightarrow BD = \left( 50 - x \right)\sqrt{3}\]
\[ \Rightarrow \sqrt{3}x = 50\left( \sqrt{3} - 1 \right)\]
\[ \Rightarrow x = \frac{50\left( \sqrt{3} - 1 \right)}{\sqrt{3}}\]
\[ \Rightarrow x = \frac{50\left( 3 - \sqrt{3} \right)}{3}\]
\[ \Rightarrow x = \frac{50\left( 3 - 1 . 732 \right)}{3}\]
\[ \Rightarrow x = 21 . 13 m \left( \text{approx} \right)\]
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
In given figure, the value of CE is ____________.