Advertisements
Advertisements
Question
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
Solution
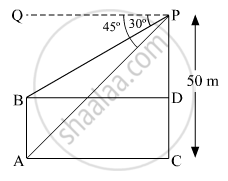
Let PC and AB represents the tower and the pole, respectively.
Suppose AB = x m.
From the above figure, we have
\[\angle PAC = \angle QPA = 45^o \left( \text{Alternate angles} \right)\]
\[\angle PBD = \angle QPB = 30^o \left( \text{Alternate angles} \right)\]
PD = PC − CD = PC − AB = (50 − x) m
In ∆PAC,
\[\tan45^o = \frac{PC}{AC}\]
\[ \Rightarrow 1 = \frac{PC}{AC}\]
\[ \Rightarrow AC = PC = 50 m\]
In ∆PBD,
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{PD}{BD}\]
\[ \Rightarrow BD = PD\sqrt{3}\]
\[ \Rightarrow BD = \left( 50 - x \right)\sqrt{3}\]
\[ \Rightarrow \sqrt{3}x = 50\left( \sqrt{3} - 1 \right)\]
\[ \Rightarrow x = \frac{50\left( \sqrt{3} - 1 \right)}{\sqrt{3}}\]
\[ \Rightarrow x = \frac{50\left( 3 - \sqrt{3} \right)}{3}\]
\[ \Rightarrow x = \frac{50\left( 3 - 1 . 732 \right)}{3}\]
\[ \Rightarrow x = 21 . 13 m \left( \text{approx} \right)\]
APPEARS IN
RELATED QUESTIONS
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
