Advertisements
Advertisements
Question
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
Options
A. `25sqrt2`
B. `25sqrt3`
C. 25
D. 12.5
Solution
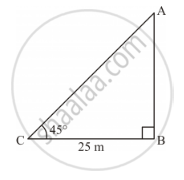
Let AB be the tower and C be the point on the ground 25 m away from the foot of the
tower such that ∠ACB = 45°.
In right ΔABC:
`tan 45 ^@=(AB)/(BC)`
`rArr l=(AB)/25m`
⇒ AB = 25 m
Thus, the height of the tower is 25 m.
The correct answer is C.
APPEARS IN
RELATED QUESTIONS
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
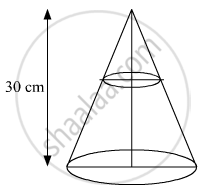
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
Find the angle of elevation of the sun when the shadow of a pole h metres high is `sqrt(3)` h metres long.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
