Advertisements
Advertisements
Question
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
Solution
Let h be the height of tower and angle of elevation of the foot of the tower is 30°, on advancing 150 m towards the foot of tower then an angle of elevation becomes 60°.
We assume that BC = x and CD = 150 m.
Now we have to prove height of the tower is 129.9 m.
So we use trigonometrical ratios.
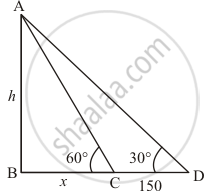
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60^@ = (AB)/(BC)`
`=> sqrt3 = h/x`
`=> h/sqrt3 = x`
Again in a triangle ABD
`=> tan D = (AB)/(BC + CD)`
`=> tan 30^@ = h/(x + 150)`
`=> 1/sqrt3 = h/(x + 150)`
`=> x + 150 = sqrt3h`
`=> x = sqrt3h - 150`
`=> h/sqrt3 = sqrt3 - 150`
`=> h = 3h - 150sqrt3`
`=> 2h = 150sqrt3`
`=> h = (150 xx 1.732)/2`
=> h = 129.9
Hence the height of tower is 129.9 m proved
APPEARS IN
RELATED QUESTIONS
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


