Advertisements
Advertisements
Question
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ
Solution
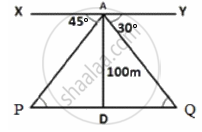
i. XY || PQ and AP is transversal.
∠APD = ∠PAX ...(Alternative interior angles)
∠APD = 45°
ii. Since XY || PQ and AQ is a transversal
So alternate interior angles are equal
Hence ∠YAQ = ∠AQD = 30°
iii. In ΔADP, θ = 45°
tan θ = `"P"/"B"`
tan 45° = `100/("PD")`
PD = 100 m
Boat P is 100 m from the light house
OR
In ΔADQ, θ = 30°
tan θ = `"P"/"B"`
tan 30° = `100/("DQ")`
`1/sqrt(3) = 100/("DQ")`
DQ = `100sqrt(3)` m
APPEARS IN
RELATED QUESTIONS
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
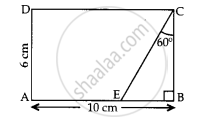
In given figure, the value of CE is ____________.
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.


