Question

From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower

Answer 1

Let AB be the building and CD be the tower.

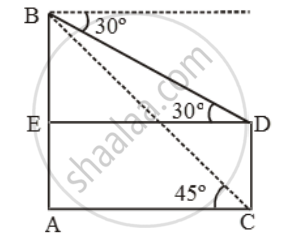
Then, AB = 30 m. Let DC = x.

Draw DE ⊥ AB. Then AE = CD = x.

∴ BE = (30 – x) m.

`\text{Now, }\frac{AC}{AB}=\text{cot 45}^\text{o}=1`

`\Rightarrow \frac{AC}{30}=1\Rightarrow AC=30 m`

∴ DE = AC = 30 m.

`\frac{BE}{DE}=\text{tan }30^\text{o}=\frac{1}{\sqrt{3}}`

`\Rightarrow\frac{BE}{30}=\frac{1}{\sqrt{3}}`

`\Rightarrow BE=\frac{30}{\sqrt{3}}`

`\therefore CD=AE=AB-BE=( 30-\frac{30}{\sqrt{3}} ) `

`=30( 1-\frac{1}{\sqrt{3}})m`