Advertisements
Advertisements
Question
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
Solution
Let BD be the width of the river. And the angle of depression of the bank on opposite side of the river is 30° and 45° respectively. It is given that AC = 30 m.
Let BC = x and CD = y. And ∠ABC = 30°, ∠ADC = 45°.
Here we have to find the width of the river.
We have the following figure
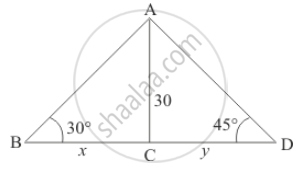
So we use trigonometric ratios.
In a triangle ABC
`=> tan 30° = (AC)/(BC)`
`=> 1/sqrt3 = 30/x`
`=> x = 30sqrt3`
Again in a triangle ADC
`=> tan 45° = (AC)/(CD)`
`=> 1 = 30/y`
`=> y = 30`
So width of river is
`x + y = 30sqrt3`
`x + y = 30(sqrt3 + 1)`
Hence the width of river is `(30(sqrt3 + 1)`m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
