Advertisements
Advertisements
Question
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
Solution
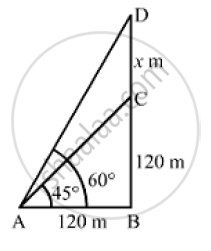
Let BC and CD be the heights of the tower and the flagstaff, respectively.
We have,
AB = 120m, ∠BAC = 45º ,∠BAD = 60°
Let CD = x
In ΔABC,
`tan 45° = (BC)/(AB)`
`⇒ 1 =(BC)/120`
`⇒ BC = 120m`
Now , in ΔABD,
` tan 60º (BD )/(AB)`
`⇒ sqrt(3)= (BC +CD)/ 120`
`⇒ BC + CD = 120 sqrt(3)`
`⇒ x = 120 sqrt( 3 )-120`
`⇒ x = 120 ( sqrt(3)-1)`
⇒ x = 120 ( 1.732 -1)
⇒ x = 120 (0.732)
`⇒ x = 87.84 ~~ 87.8m`
So, the height of the flagstaff is 87. 8 m.
APPEARS IN
RELATED QUESTIONS
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
The Distance of the point (−3, 4) from the x-axis is
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
