Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
उत्तर
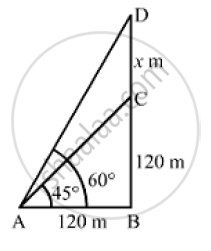
Let BC and CD be the heights of the tower and the flagstaff, respectively.
We have,
AB = 120m, ∠BAC = 45º ,∠BAD = 60°
Let CD = x
In ΔABC,
`tan 45° = (BC)/(AB)`
`⇒ 1 =(BC)/120`
`⇒ BC = 120m`
Now , in ΔABD,
` tan 60º (BD )/(AB)`
`⇒ sqrt(3)= (BC +CD)/ 120`
`⇒ BC + CD = 120 sqrt(3)`
`⇒ x = 120 sqrt( 3 )-120`
`⇒ x = 120 ( sqrt(3)-1)`
⇒ x = 120 ( 1.732 -1)
⇒ x = 120 (0.732)
`⇒ x = 87.84 ~~ 87.8m`
So, the height of the flagstaff is 87. 8 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
