Advertisements
Advertisements
प्रश्न
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
उत्तर
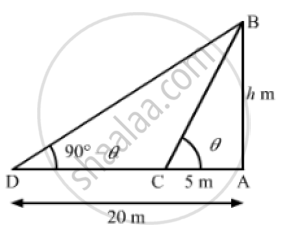
Let the height of the tower be AB.
We have.
AC = 5m, AD = 20m
Let the angle of elevation of the top of the tower (i.e. ∠ACB) from point C be θ .
Then,
the angle of elevation of the top of the tower (i.e. Z ADB) from point D
=(90° -θ)
Now, in ΔABC
`tan theta = (AB)/(AC)`
`⇒ tan theta = (AB)/5` ...................(i)
Also, in ΔABD,
`cot (90° - theta ) = (AD)/(AB)`
`⇒ tan theta = 20/(AB)` .................(ii)
From (i) and (ii), we get
`(AB)/5 = 20/(AB)`
`⇒ AB^2 = 100`
`⇒ AB = sqrt(100)`
∴ AB = 10 m
So, the height of the tower is 10 m.
APPEARS IN
संबंधित प्रश्न
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
