Advertisements
Advertisements
प्रश्न
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
उत्तर
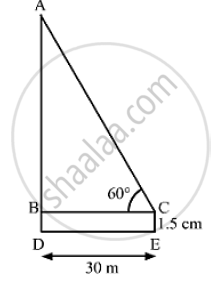
Let CE and AD be the heights of the observer and the chimney, respectively.
We have,
BD = CE = 1.5 m, BC = DE = 30 mand ∠ACB = 60°
In ΔABC
`tan 60° = (AB)/(BC)`
`⇒ sqrt(3 ) = (AD-BD)/30`
`⇒ AD -1.5 =30 sqrt(3)`
`⇒ AD = 30sqrt(3) +1.5`
`⇒ AD = 30XX 1.732 + 1.5`
`⇒ AD = 51.96 + 1.5`
`⇒ AD = 53.46 m`
So, the height of the chimney is 53.46 m (approx).
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
In given figure, the value of CE is ____________.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
