Advertisements
Advertisements
प्रश्न
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
उत्तर
Let OX be the horizontal ground and A be the position of the kite.
Also, let O be the position of the observer and OA be the thread.
Now, draw AB ⊥ OX.
We have:
∠BOA= 60°,OA= 75m and ∠OBA = 90°
Height of the kite from the ground = AB = 75 m
Length of the string OA = xm
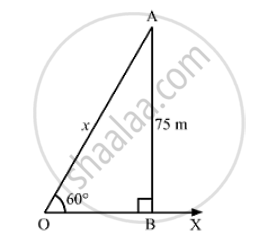
In the right ΔOBA,we have:
`(AB)/(OA ) = sin 60° = sqrt(3)/2`
`⇒ 75/x = sqrt(3)/2`
`⇒ x = (75xx2)/sqrt(3) = 150/1.732 = 86.6m`
Hence, the length of the string is 86.6m
APPEARS IN
संबंधित प्रश्न
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
