Question

The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.

Answer 1

Let h be the height of tower AB and angle of elevation are 45° and 60° are given.

In a triangle OAC, given that AB = 10+x and BC = x

Now we have to find the height of the tower.

So we use trigonometrical ratios.

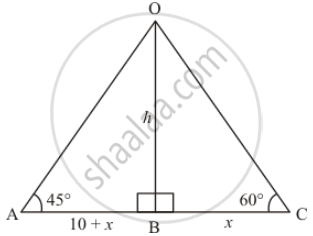
In a triangle OAB,

`=> tan A = (OB)/(AB)`

`=> tan 45^@ = (OB)/(AB)`

`=> 1= h/(10 + x)`

=> h = 10 + x

Therefore  x = h - 10

Again in a triangle OCB

`=> tan C = (OB)/(BC)`

`=> tan 60^@ = (OB)/(BC)`

`=> sqrt3 = h/x`

`=> h = sqrt3x`

Put x = h - 10

`=> h = sqrt3 (h - 10)`

`=> h = sqrt3h - 10sqrt3`

`=> 10sqrt3 = h(sqrt3 - 1)`

`=> h = (10sqrt3)/(sqrt3 - 1)`

`=>  h = (10 xx 1.732)/(1.732 - 1)`

`=> h = 17.32/0.327`

=> h = 23.66

Hence height of tower is 23.66 m