Advertisements
Advertisements
Question
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
Solution
Let h be the height of tower AB and angle of elevation are 45° and 60° are given.
In a triangle OAC, given that AB = 10+x and BC = x
Now we have to find the height of the tower.
So we use trigonometrical ratios.
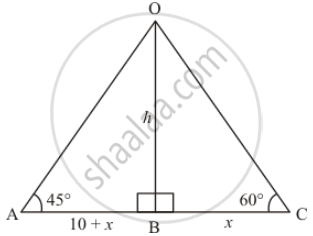
In a triangle OAB,
`=> tan A = (OB)/(AB)`
`=> tan 45^@ = (OB)/(AB)`
`=> 1= h/(10 + x)`
=> h = 10 + x
Therefore x = h - 10
Again in a triangle OCB
`=> tan C = (OB)/(BC)`
`=> tan 60^@ = (OB)/(BC)`
`=> sqrt3 = h/x`
`=> h = sqrt3x`
Put x = h - 10
`=> h = sqrt3 (h - 10)`
`=> h = sqrt3h - 10sqrt3`
`=> 10sqrt3 = h(sqrt3 - 1)`
`=> h = (10sqrt3)/(sqrt3 - 1)`
`=> h = (10 xx 1.732)/(1.732 - 1)`
`=> h = 17.32/0.327`
=> h = 23.66
Hence height of tower is 23.66 m
APPEARS IN
RELATED QUESTIONS
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
