Advertisements
Advertisements
Question
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
Solution
Let h be the height of aeroplane p above the road.
And A and B be the two consecutive milestones, then AB = 1 mile. we have ∠PAQ = α and ∠PBQ = β.
We have to prove
`h = (tan alpha tan beta)/(tan alpha + tan beta)`
The corresponding figure is as follows
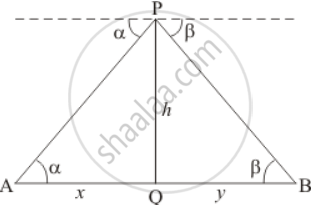
In ΔPAQ
`=> tan alpha = (PQ)/(AQ)`
`=> tan alpha = h/x`
`=> x = h/(tan alpha)`
`=> x = h cot alpha`
Again in ΔPBQ
`=> tan beta =(PQ)/(BQ)`
`=> tan beta = h/y`
`=> y = h/(tan beta)`
`=> y = h cot beta`
Now,
`=> AB = x + y`
`=> AB = h(cot alpha + cot beta)`
`=> AB = h(1/tan alpha + 1/tan beta)`
`=> AB = h((tan alpha + tan beta)/(tan alpha tan beta))`
Therefore `h = (tan alpha tan beta)/(tan alpha + tan beta)` (Since A B = 1)
Hence height of aero plane is `(tan alpha tan beta)/(tan alpha + tan beta)`
APPEARS IN
RELATED QUESTIONS
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
