Advertisements
Advertisements
Question
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
Solution
Let C′ be the image of cloud C. We have ∠CAB = α and ∠BAC' = β
Again let BC = x and AC be the distance of cloud from point of observation.
We have to prove that
`AC= (2h sec alpha)/(tan beta - tan alpha)`
The corresponding figure is as follows
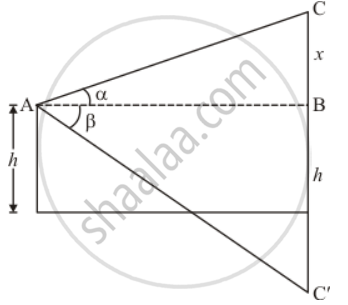
We use trigonometric ratios.
in Δ ABC
`=> tan alpha = (BC)/(AB)`
`=> tan alpha = x/(AB)`
Again in Δ ABC'
`=> tan beta = (BC')/(AB)`
`=> tan beta = (x + 2h)/(AB)`
Now
`=> tan beta - tan alpha = (x + 2h)/(AB) - x/(AB)`
`=> tan bea - tan alpha = (2h)/(AB)`
`=> AB = (2h)/(tan beta - tan alpha)`
Again in Δ ABC
`=> cos alpha = (AB)/(AC)`
`=> AC = (AB)/(cos alpha)`
`=> (2h sec alpha)/(tan beta - tan alpha)`
Hence distance of cloud from points of observation is `(2h sec alpha)/(tan beta - tan alpha)`
APPEARS IN
RELATED QUESTIONS
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
The banks of a river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line inclined to the bank at 45º and reaches the opposite bank at a point 20 m from the point opposite to the starting point. Find the breadth of the river
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
