Advertisements
Advertisements
Question
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
Solution
Let AB be the surface of lake and P be the point of observation such that AP = 2500 m. Let C be the position of cloud and C' be the reflection in the lake. Then CB = C'B
Let PQ be the perpendicular from P on CB.
Let PQ = x m, CQ = h, QB = 2500 m. then CB = h + 2500 consequently C'B = h + 2500 m. and ∠CPQ - 15°, .∠QPC' = 45°

Here we have to find the height of cloud.
We use trigonometric ratios.
In ΔPCQ
`=> tan 15° = (CQ)/(PQ)`
`=> 2 - sqrt3 = h/x`
`=> x = h/(2 - sqrt3)`
Again in Δ PQC
`=> tan 45^@ = (QB + BC')/(PQ)`
`=> 1 = (2500 + h + 2500)//x`
`=> x = 5000 } h`
`=> h /()2 - sqrt3 = 5000 + h`
`=> h = 2500 (sqrt3 - 1)`
`=> CB = 2500 + 2500 (sqrt3 - 1)`
`=> CB = 2500sqrt3`
Hence the height of cloud is `2500sqrt3` m
APPEARS IN
RELATED QUESTIONS
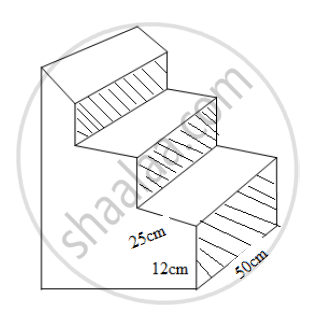
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
