Advertisements
Advertisements
Question
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
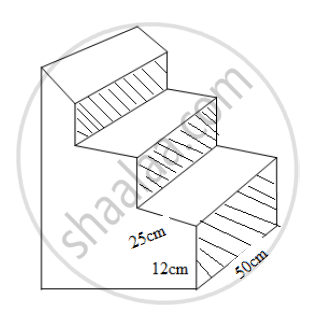
Solution
The 1 st stair-step=h1=12 cm.
The 2 nd stair-step=h2=24 cm.
The 3 rd stair-step=h3=36 cm.
The total height=h= h1+ h2+ h3= 12 + 24 + 36 = 72 cm.
Length and width will remain same.
Length=l=50 cm
Width=w=25 cm
The volume of the three stair-step=Length(l) × Width(w) × Height(h)
The volume of the three stair-step=50 × 25 × 72 cu.cm
Given: The volume of 1 brick = 12.5 × 6.25 × 4 cu.cm
Let the number of bricks required be n.
(12.5 × 6.25 × 4) × n = 50 × 25× 72
`n=(50xx25xx72)/(12.5xx6.25xx4)=288`
288 bricks are used in three stair-steps.
APPEARS IN
RELATED QUESTIONS
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The distance of point A(-5, 6) from the origin is ______.
When the length of shadow of a vertical pole is equal to `sqrt3` times its height, the angle of elevation of the Sun’s altitude is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
