Advertisements
Advertisements
Question
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
Solution
Let AB be the flag of length hm on the building BC.
We assume that BC = 10, ∠APC = 45°, ∠BPC = 30°
Now we have to find height of flag-staff and distance of the point P from the building
The corresponding figure is as follows
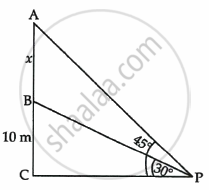
In a triangle BPC,
`=> tan "P" = ("BC")/("CP")`
`=> tan 30^@ = ("BC")/("CP")`
`=> "CP"="BC"/tan30^@`
`=> 10/(1/sqrt3)`
`= 10sqrt3` m
Again in a triangle ACP
`=> tan "P" = ("AC")/"CP"`
`=> 1 = ("AC")/"CP"`
`=>` AC = CP = 10`sqrt3` m
`=>` AB + BC = CP
`=>` x = 10 = 10`sqrt3`
`=> x = 10sqrt3-10`
`=>10(sqrt3-1)`
= 10 × 0.73
h = 7.32
Hence the length is 17.32 m and distance is 7.32 m
APPEARS IN
RELATED QUESTIONS
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
