Advertisements
Advertisements
Question
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
Solution
Let AC be the lamp post of height h
We assume that ED = 1.6 m, BE = 4.8 m and EC = 3.2 m
We have to find the height of the lamp post
Now we have to find the height of lamp post using similar triangles.
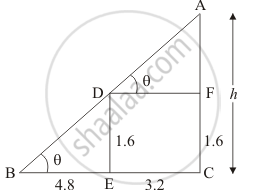
Since triangle BDE and triangle ABC are similar.
`(AC)/(BC) = (ED)/(BE)`
`h/(4.8 + 3.2) = 1.6/(BE)`
`h = 8/3`
Again, we have to find height of lamp post using trigonometric ratios.
In ΔADE
`=> tan theta = 1.6/4.8`
`=> tan theta = 1/3`
Again in ΔABC
`=> tan theta = h/(4.8 + 3.2)`
`=> 1/2 = h/8`
`h = 8/3`
Hence the height of lamp post is 8/3 m
APPEARS IN
RELATED QUESTIONS
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
