Advertisements
Advertisements
Question
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
Solution 1
Let AB be the building of height 60 and CD be the lamp post of height h, an angle of depression of the top and bottom of vertical lamp post is 30° and 60° respectively.
Let AE = h, AC = x, and AC = ED.
it is also given AB = 60 m. Then BE = 60 - h And
∠ACB = 60°, ∠BDE = 30°
We have to find the following
(1) The horizontal distance between AB and CD
(2) The height of lamp post
(3) The difference between the heights of building and the lamp post
We have the corresponding figure as follows
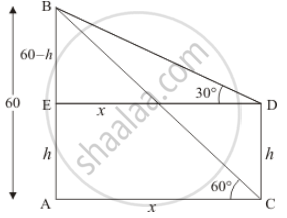
1) So we use trigonometric ratios.
In Δ ABC
`=> tan 60° = (AB)/(AC)`
`=> sqrt3 = 60/x`
`=> x = 60/sqrt3`
`=> x = 34.64`
Hence the distance between AB and CD is 34.64
2) Again in Δ BDE
`=> tan 30^@ = (BE)/(DE)`
`=> 1/sqrt3 = (60 - h)/x`
`=> 60/sqrt3 = (60 - h) sqrt3`
`=> 60 = 180 - 3h`
`=> 3h = 180 - 60`
`=> 3h = 120`
`=> h = 40`
Hence the height of lamp post is 40 m
3) SInce BE= 60 - h
=> BE = 60 - 40
=> BE = 20
Hence the difference between height of building and lamp post is 20 m
Solution 2
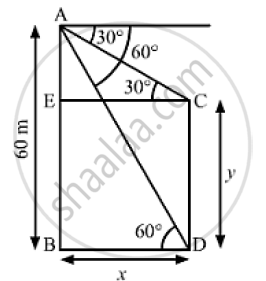
We have,
AB = 60m, ∠ACE = 30° and ∠ADB = 60°
Let BD =CE = x and CD = BE = y
⇒ AE = AB - BE = 60 - y
In ΔACE,
`tan 30° = (AE)/(CE)`
`⇒ 1/ sqrt(3) = (60-y)/x`
`⇒ x = 60 sqrt(3)- y sqrt(3)` ............(1)
Also in ,Δ ABD,
`⇒ tan 60° = (AB)/(BD)`
`⇒ sqrt(3) = 60/x`
`⇒ x = 60/ sqrt(3)`
`⇒ x = 60/ sqrt( 3) xx sqrt(3) / sqrt(3)`
`⇒x = (60- sqrt(3))/3`
`⇒ x = 20 sqrt(3)`
Substituting x =20` sqrt(3)` in (i), we get
`20 sqrt(3) = 60 sqrt(3) - ysqrt(3)`
`⇒ y sqrt(3) = 60 sqrt(3) - 20 sqrt(3)`
`⇒y sqrt(3) = 40 sqrt(3) `
`⇒ y = ( 40 sqrt(3))/sqrt(3)`
⇒ y = 40 m
(i) The horizontal distance between AB and CD = BD = x
`= 20 sqrt(3)`
= 20×1.732
=34.64 m
(ii) The height of the lamp post = CD = y = 40m
(iii) the difference between the heights of the building and the lamp post
=AB-CD=60-40=20m
RELATED QUESTIONS
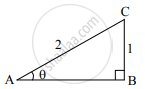
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
