Advertisements
Advertisements
Question
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
Solution
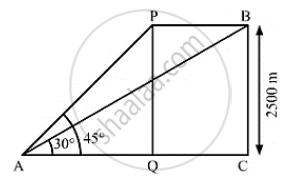
Let the height of flying of the aero-plane be PQ = BC and point A be the point of observation.
We have,
PQ = BC = 2500m, ∠PAQ = 45° and ∠BAC = 30°
In ΔPAQ,
` tan 45° = (PQ)/(AQ)`
`⇒ 1 = 2500/(AQ)`
`⇒AQ = 2500 m`
Also, in ΔABC,
`tan 30° = (BC)/(AC)`
`⇒1/ sqrt(3) = 2500/(AC)`
`⇒ AC = 2500 sqrt(3) m`
Now , QC = AC - AQ
`= 2500 sqrt(3)-2500`
`= 2500( sqrt(3)-1) m`
`= 2500 (1.732 - 1)`
`= 2500(0.732)`
`= 1830 m`
⇒ PB = QC = 1830
So, the speed of the aero-plane`(PB)/15`
`= 1830/15`
=122 m/s
`=122 xx3600/1000 km ⁄ h`
= 439.2 km /5
So, the speed of the aero-plane is 122m/ s or 439.2 km/ h.
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
Find the distance between the points (a, b) and (−a, −b).
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

