Advertisements
Advertisements
Questions
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution 1
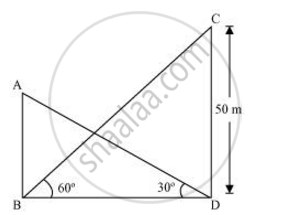
Let AB be the building and CD be the tower.
In ΔCDB,
`"CB"/"BD"` = tan 60°
`50/("BD") = sqrt3`
`"BD" = 50/sqrt3`
In ΔABD,
`("AB")/("BD") = tan 30°`
AB = `50/sqrt3 xx 1/sqrt3`
= `50/3`
= `16 2/3`
Therefore, the height of the building is `16 2/3` m.
Solution 2
Let AD be the building of height h m. and an angle of elevation of the top of building from the foot of the tower is 30° and an angle of the top of the tower from the foot of building is 60°.
Let AD = h, AB = x and BC = 50 and ∠DBA = 30°, ∠CAB = 60°
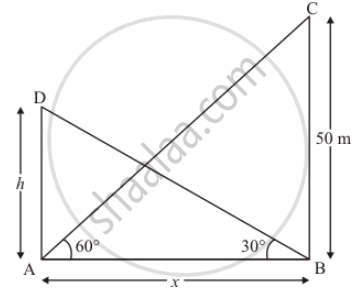
So we use trigonometric ratios.
In a triangle ABC
⇒ `tan 60° = 50/x`
⇒ `sqrt3 = 50/x`
⇒ `x = 50/sqrt3`
Again in a triangle ABD
⇒ `tan 30° = ("AD")/("AB")`
⇒ `1/sqrt3 xx h/x`
⇒ `h = x/sqrt3`
⇒ `h = 50/(sqrt3 xx sqrt3)`
⇒ `h = 50/3`
⇒ `h =16 2/3`
Therefore, the height of the building is `16 2/3` m.
RELATED QUESTIONS
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
