Advertisements
Advertisements
Question
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
Solution
Let CD be the tower. A and B are the two points on the same side of the tower.
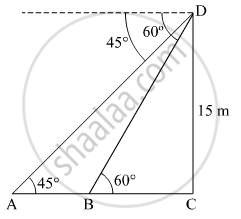
In ΔDBC
`tan 60^@ = (DC)/(BC)`
`=> sqrt3 = 15/(BC)`
`=> BC = 15/sqrt3`
`=> BC = 5sqrt3 m`
In ΔDAC
`tan 45^@ = (DC)/(AC)`
`=> 1 = 15/"AC"`
`=> AC = 15 m`
Now
AC = AB + BC
`:. AB = AC - BC = 15 - 5sqrt3 = 5(3 - sqrt3) m`
Hence, the distance between the two points A and B is `5(3 - sqrt3) m`
APPEARS IN
RELATED QUESTIONS
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
