Advertisements
Advertisements
Question
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
Solution
Let H be the height of the pole, makes an angle of depression from the top of the tower to top and bottom of\ poles are 45° and 60° respectively.
Let AB = H , CE = h, AD = x and DE = 50m.
`∠CBE = 45^@ and ∠DAE = 60^@`
Here we have to find height of pole.
The corresponding figure is as follows
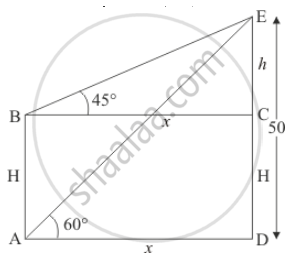
In ΔADE
`=> tan A = (DE)/(AD)`
`=> tan 60^@ = 50/x`
`=> x = 50/sqrt3`
Again in ΔBCE
`=> tan B = (CE)/(BC)`
`=> tan 45^@ = h/x`
`=> 1 = h/x`
`=> h = 50/sqrt3`
`=> h = 28.87`
Therefore H = 50 - h
=> H = 50 - 28.87
`=> H = 21.13`
Hence height pole is 21.13 m
APPEARS IN
RELATED QUESTIONS
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
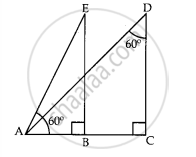
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
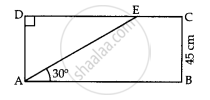
In given figure, the value of AE is ____________.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
