Advertisements
Advertisements
Question
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
Solution
Let AB represents the unbroken part and AC represent the broken part of the tree. The top of the tree (T) touches the ground at C.
BC = 30 cm, `angleACB = 30^@`
Total height of the tree = AB + AT = AB + AC .....(1)
In right angles `triangleABC`,
`tan angleACB = "AB"/"BC"`
`:. tan30^@ = "AB"/"BC"`
`:. 1/sqrt3 = (AB)/30`
`:. AB = 30/sqrt3 m` ......(2)
Also `cos angleACB = (BC)/(AC)`
`:. cos30^@ = (BC)/(AC)`
`:. sqrt3/3 = 30/(AC)`
`:.AC = 30 xx 2/sqrt3`
`:. AC = 60/sqrt3`
`:. AT = 60/sqrt3` ...(3)
Height of the tree = AB + AT ...[From (1)]
`= 30/sqrt3 + 60/sqrt3` ...[From (2) and (3)]
`=(30+60)/sqrt3 = 90/sqrt3 = 90/sqrt3 xx sqrt3/sqrt3 = (90sqrt3)/3`
∴ the height of the tree = `30sqrt3` m
= `30 xx 1.73 m` = 51.90 m
The height of the whole tree is 51.90 m.
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
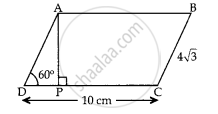
In given figure, ABCD is a || gm. The length of AP is ____________.
An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Find the angle of elevation of the sun when the shadow of a pole h metres high is `sqrt(3)` h metres long.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
