Advertisements
Advertisements
Questions
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a triangle ABC. Find the equation of median AD
Solution 1
AD is the median
∴ CD BD ... (∵ D is the midpoint of BC)
Coordinates of D can be found by using section formula.
Let (x,y) be coordinates of the centre of the circle.
`(x,y)=((1-3)/(1+1),(-8-2)/(1+1))=(-1,-5)`
Coordinates of point D are (-1,-5)
Let m be the slope of AD.
Coordinates of A(5, 4) and D(–1, –5)
`m=(y_2-y_1)/(x_2-x_1)=(4-(-5))/(5-(-1))=9/6=3/2`
Equation of line is y = mx+c, where c is the y int ercept.
`4=(3 xx 5)/2+c ...(" Substituting the coordinates of A ")`
c=-7/2
Equation of line of AD is
`y="3x"/2-7/2`
2y =3x - 7 is equation of the median AD.
The coordinates of A (5,4) and C (1, -8)
Slope of AC = `(y_2-y_1)/(x_2-x_1)=-12/-4=3`
Substituting the coordinates of A(5,4) in the equation y = mx + c
4 = (3x5)+c
c=-11
Line parallel to AC and pas sing through B(-3, -2) has slope 3
Substituting the coordinates of B 3, 2 in the equation y=mx+c
-2=(3x -3)+c
c=7
Equation of line parallel to AC and passing through B(-3,-2) is y=3x+7
Solution 2
Let A(5,4) ≡ `(x_1,y_1)`; B(-3, -2) ≡ `(x_2,y_2)` and C(1,-8) ≡ `(x_3,y_3)`
D(x, y) is the midpoint of BC.
∴ the coordinates of `D = ((x_2 + x_3)/2, (y_2+y+_3)/2)`
`= ((-3+1)/2, (-2-8)/2) = (-2/2, -10/2) = (-1,-5)`
Let D(-1,-5) ≡ `(x_4,y_4)`
The equation of median AD is
`(x - x_1)/(x_1-x_4) = (y - y_1)/(y_1 - y_4)`
`:. (x-5)/(5-(-1)) = (y-4)/(4-(-5))`
`:. (x-5)/(5+1) = (y-4)/(4+5)`
`:. (x - 5)/6 = (y-4)/9`
`:. (x-5)/2 = (y -4)/3`
Multiplying both the sides by 6,
3(x - 5) = 2(y - 4) ∴ 3x - 15 = 2y - 8
∴ 3x - 2y - 15 + 8 = 0 ∴ 3x - 2y - 7 = 0
APPEARS IN
RELATED QUESTIONS
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
ax – by = 0
Find the slope and y-intercept of the line:
3x – 4y = 5
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
Match the equations A, B, C and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A ≡ y = 2x;
B ≡ y – 2x + 2 = 0;
C ≡ 3x + 2y = 6;
D ≡ y = 2
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Find:
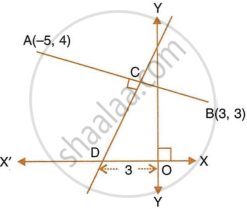
- equation of AB
- equation of CD
Find Equation of CD
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
