Advertisements
Advertisements
Question
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Solution
Distance between two points = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
By distance formula,
`"PQ" = sqrt([2 - (-2)]^2 + (2 - 2)^2)`
`"PQ" = sqrt((2 + 2)^2 + (0)^2)`
`"PQ" = sqrt((4)^2)`
PQ = 4 ...(i)
`"QR" = sqrt((2 - 2)^2 + (7 - 2)^2)`
`"QR" = sqrt((0)^2 + (5)^2)`
`"QR" = sqrt((5)^2)`
QR = 5 ...(ii)
`"PR" = sqrt([2 - (-2)]^2 + (7 - 2)^2)`
`"PR" = sqrt((2 + 2)^2 + (5)^2)`
`"PR" = sqrt((4)^2 + (5)^2)`
`"PR" = sqrt(16 + 25)`
`"PR" = sqrt(41)`
Now, PR2 = `(sqrt(41))^2` = 41 ...(iii)
From (i) and (ii),
∴ PQ2 + QR2 = 42 + 52 = 16 + 25 = 41
∴ PR2 = PQ2 + QR2 ...[From (iii)]
∴ ΔPQR is a right angled triangle. ...[Converse of Pythagoras theorem]
∴ Point P, Q, and R are the vertices of a right angled triangle.
APPEARS IN
RELATED QUESTIONS
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Given 3x + 2y + 4 = 0
(i) express the equation in the form y = mx + c
(ii) Find the slope and y-intercept of the line 3x + 2y + 4 = 0
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
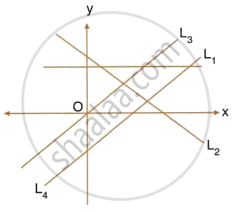
Match the equations A, B, C and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A ≡ y = 2x;
B ≡ y – 2x + 2 = 0;
C ≡ 3x + 2y = 6;
D ≡ y = 2
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
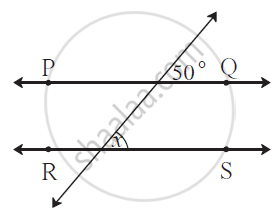
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
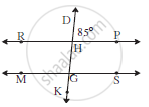
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
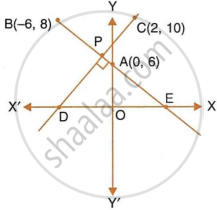
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
If (4,-3) is a point on line 5x +8y = c, find the value of c.
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
