Advertisements
Advertisements
Question
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.
Solution
x-intercept of the line = –3
∴ Required line passes through (–3, 0) and is perpendicular to the line
3x + 5y = 1
5y = 1 – 3x
= –3x + 1
`y = -3/5 x + 1/5`
∴ Slope `m = -3/5`
Slope of the line perpendicular to the given line = `(+5)/3`
∴ Equation of the required line through = (–3, 0) and having slope `5/3` is given by
`y - 0 = 5/3(x + 3)`
`\implies` 3y = 5x + 15
`\implies` 5x – 3y + 15 = 0
APPEARS IN
RELATED QUESTIONS
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
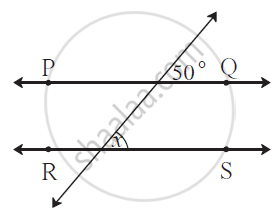
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
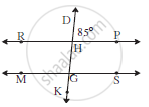
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
If (4,-3) is a point on line 5x +8y = c, find the value of c.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
