Advertisements
Advertisements
Question
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Solution
Given equation of a line is x − y = 4
`=>` y = x − 4
Comparing this equation with y = mx + c, we have:
Slope = m = 1
y-intercept = c = −4
Let the inclination be θ.
Slope = 1 = tan θ = tan 45°
∴ θ = 45°
APPEARS IN
RELATED QUESTIONS
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
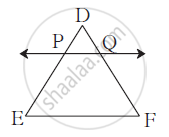
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
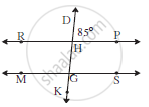
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
If (4,-3) is a point on line 5x +8y = c, find the value of c.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
