Advertisements
Advertisements
Question
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
Solution
For the point A (the point on x-axis), the value of y = 0.
4x – 3y + 12 = 0
Co-ordinates of point A are (–3, 0)
Here, (x1, y1) = (–3, 0)
The given line is 4x – 3y + 12 = 0
3y = 4x + 12
Slope of this line =
∴ Slope of a line perpendicular to the given line
=
=
Required equation of the line passing through A is
y − y1 = m(x − x1)
4y = −3x − 9
3x + 4y + 9 = 0
APPEARS IN
RELATED QUESTIONS
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
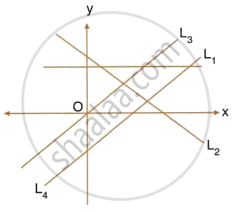
Match the equations A, B, C and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A ≡ y = 2x;
B ≡ y – 2x + 2 = 0;
C ≡ 3x + 2y = 6;
D ≡ y = 2
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
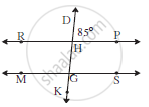
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
