Advertisements
Advertisements
Question
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
Solution
Let (2, 3) ≡ (x1, y1) and (4, 7) ≡ (x2, y2).
The equation of a line passing through a pair of points is
m = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
`= (7-3)/(4-2) = 4/2 = 2`
Here, I have two points, which I used to find the slope. Now I need to pick one of the points (it doesn't matter which one), and use it to solve for b
Using the point (2,3), I get :
y = mx + b
3 = 2(2) + b
3 = 4 + b
3 - 4 = b
b = -1
So , y = 2x - 1
On the other hand, if I use the point (4,7), I get:
y = mx + b
7 = 2(4) + b
7 = 8 + b
7 - 8 = b
b = -1
then y = 2x - 1
So it doesn't matter which point I choose. Either way, the answer is the same : y = 2x - 1
APPEARS IN
RELATED QUESTIONS
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Find the slope and y-intercept of the line:
ax – by = 0
Find the slope and y-intercept of the line:
3x – 4y = 5
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Find the equation of the line which is perpendicular to the line `x/a - y/b = 1` at the point where this line meets y-axis.
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
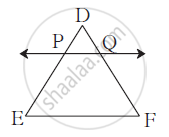
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
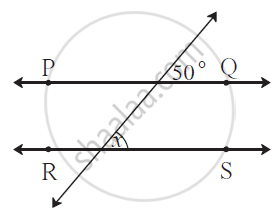
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
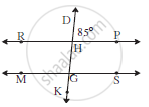
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find:
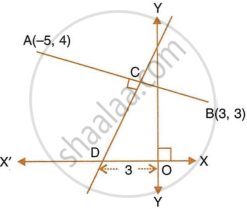
- equation of AB
- equation of CD
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
