Advertisements
Advertisements
Question
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Solution 1
Given: A circle with centre O and an external point P are given.
AP and BP are the two tangents drawn from an external point P.

To prove: AP = BP
Construction: Draw seg OA, seg OB and seg OP.
Proof: In ΔOBP and ΔOAP,
OA = OB … (Radii of the same circle)
OP = OP … (Side common to both the triangles)
∠OAP = ∠OBP = 90° … (tangent is perpendicular to the radius at the point of contact)
ΔOBP ≅ ΔOAP … (By R.H.S)
∴ AP = BP … (corresponding sides of congruent triangles)
Thus, the lengths of two tangent segments to a circle drawn from an external point are equal.
Solution 2
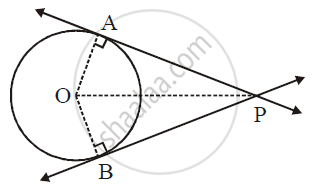
Given: O is the centre of the circle and P is a point in the exterior of the circle. A and B are the points of contact of the two tangents from P to the circle.
To Prove: PA = PB
Construction: Draw seg OA, seg OB and seg OP.
Proof: Line AP ⊥ radius OA and line BP ⊥ radius OB ... (Tangent perpendicular to radius)
∴ `anglePAO = anglePBO = 90^@`
In right-angled triangles `triangle OAP` and `triangleOBP`
hypotenuse OP ≅ hypotenuse OP ...(Common side)
seg OA ≅ seg OB ...(Radii of the same circle)
`:.triangleOAP ≅ triangleOBP` ...(Hypotenuse-side of theorem)
∴ seg PA ≅ seg PB ...(c.s.c.t.)
∴ PA = PB
APPEARS IN
RELATED QUESTIONS
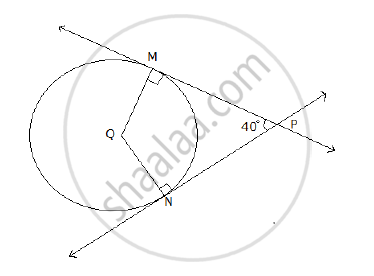
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
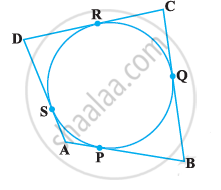
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that a parallelogram circumscribing a circle is a rhombus.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The length of tangents drawn from an external point to the circle ______
The length of the tangent from an external point P on a circle with centre O is ______
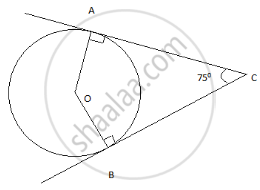
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
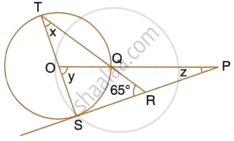
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
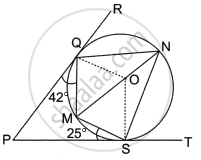
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
