Advertisements
Advertisements
Question
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Solution
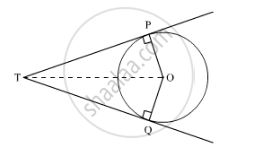
Given:
TP and TQ are two tangents drawn from an external point T to the circle C (O, r).
To prove: TP = TQ
Construction: Join OT.
Proof:
We know that a tangent to the circle is perpendicular to the radius through the point of contact.
∴ ∠OPT = ∠OQT = 90°
In ΔOPT and ΔOQT,
OT = OT ...(Common)
OP = OQ ...(Radius of the circle)
∠OPT = ∠OQT ...(90°)
∴ ΔOPT ≅ ΔOQT ...(RHS congruence criterion)
⇒ TP = TQ ...(CPCT)
Hence, the lengths of the tangents drawn from an external point to a circle are equal.
APPEARS IN
RELATED QUESTIONS
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
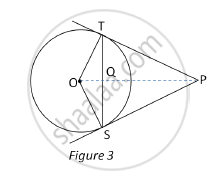
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
Prove that a parallelogram circumscribing a circle is a rhombus.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°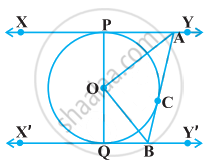
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

