Advertisements
Advertisements
प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
उत्तर
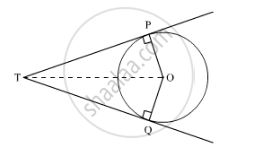
Given:
TP and TQ are two tangents drawn from an external point T to the circle C (O, r).
To prove: TP = TQ
Construction: Join OT.
Proof:
We know that a tangent to the circle is perpendicular to the radius through the point of contact.
∴ ∠OPT = ∠OQT = 90°
In ΔOPT and ΔOQT,
OT = OT ...(Common)
OP = OQ ...(Radius of the circle)
∠OPT = ∠OQT ...(90°)
∴ ΔOPT ≅ ΔOQT ...(RHS congruence criterion)
⇒ TP = TQ ...(CPCT)
Hence, the lengths of the tangents drawn from an external point to a circle are equal.
APPEARS IN
संबंधित प्रश्न
Prove that a parallelogram circumscribing a circle is a rhombus.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
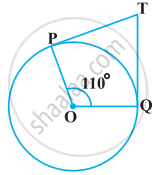
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

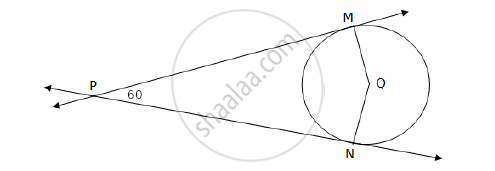
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

