Advertisements
Advertisements
प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
उत्तर
Let l be the length of the longer side and b be the length of the shorter side.
Given that the length of the diagonal of the rectangular field is 16 metres more than the shorter side.
Thus, diagonal = 16 + b
Since longer side is 14 metres more than shorter side, we have,
l= 14 + b
Diagonal is the hypotenuse of the triangle.
Consider the following figure of the rectangular field.
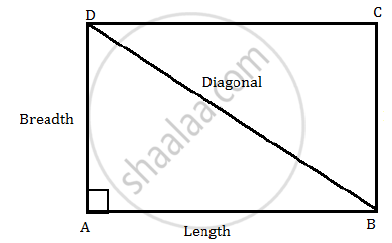
By applying Pythagoras Theorem in ΔABD, we have,
Diagonal2= Length2 +Breadt2
`(16+b)^2=(14+b)^2+b^2`
`256+b^2+32b=196+b^2+28b+b^2`
`256+32b=196+28b+b^2`
`b^2-4b-60=0`
`b^2-10b+6b-60=0`
b(b-10)+6(b-10)=0
(b+6)(b-10)=0
b=-6,b=10
As breadth cannot be negative, breadth = 10 m
Thus, length of the rectangular field = 14 + 10 = 24 m
APPEARS IN
संबंधित प्रश्न
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.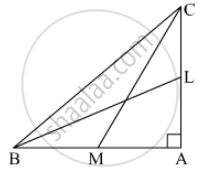
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
