Question

The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.

Answer 1

Let l be the length of the longer side and b be the length of the shorter side.
Given that the length of the diagonal of the rectangular field is 16 metres more than the shorter side.
Thus, diagonal = 16 + b
Since longer side is 14 metres more than shorter side, we have,
l= 14 + b
Diagonal is the hypotenuse of the triangle.
Consider the following figure of the rectangular field.

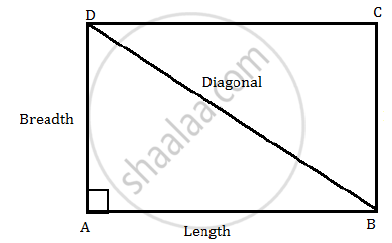
By applying Pythagoras Theorem in ΔABD, we have,
Diagonal²= Length² +Breadt²

`(16+b)^2=(14+b)^2+b^2`

`256+b^2+32b=196+b^2+28b+b^2`

`256+32b=196+28b+b^2`

`b^2-4b-60=0`

`b^2-10b+6b-60=0`

b(b-10)+6(b-10)=0

(b+6)(b-10)=0

b=-6,b=10

As breadth cannot be negative, breadth = 10 m
Thus, length of the rectangular field = 14 + 10 = 24 m