Question

D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE²

Answer 1

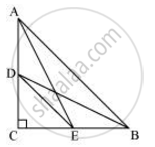
Applying Pythagoras theorem in ΔACE, we obtain

AC² + CE² = AE² ....(i)

Applying Pythagoras theorem in ΔBCD, we get

BC² + CD² = BD² ....(ii)

Using equations (i) and (ii), we get

AC² + CE² + BC² + CD² = AE² + BD² ...(iii)

Applying Pythagoras theorem in ΔCDE, we get

DE² = CD² + CE²

Applying Pythagoras theorem in ΔABC, we get

AB² = AC² + CB²

Putting these values in equation (iii), we get

DE² + AB² = AE² + BD².