Advertisements
Advertisements
प्रश्न
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

उत्तर
Applying Pythagoras theorem for ΔACD, we obtain
AC2 = AD2 +DC2
AD2 = AC2 - DC2 ... (1)
Applying Pythagoras theorem in ΔABD, we obtain
AB2 = AD2 + DB2
AD2 = AB2 - DB2 ...(2)
From equation 1 and 2 we obtain
AC2 - DC2 = AB2 - DB2 ....(3)
it is given that 3DC = DB
`:.DC = (BC)/4 `
Putting these value in equation 3 we obtain
`(AC)^2 - ((BC)/4) ^2 = (AB)^2 - ((3BC)/4)^2`
`(AC)^2 - (BC)^2/16 = (AB)^2-`
16AC2 - BC2 = 16AB2 - 9BC2
16AB2 - 16AC2 8BC2
2AB2 = 2AC2 + BC2
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
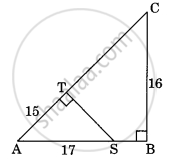
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
