Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
उत्तर
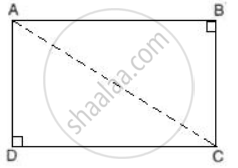
In quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
So, ΔABC and ΔADC are right-angled triangles.
In ΔABC, using Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AB2 = AC2 - BC2 ....(i)
In ΔADC, using Pythagoras theorem,
AC2 = AD2 + DC2 ....(ii)
LHS = 2AC2 - AB2
= 2AC2 - ( AC2 - BC2 ) .....[ From(i) ]
= 2AC2 - AC2 + BC2
= AC2 + BC2
= AD2 + DC2 + BC2 ....[ From(ii) ]
= RHS
APPEARS IN
संबंधित प्रश्न
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Use the information given in the figure to find the length AD.

Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
Find the unknown side in the following triangles
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

Two rectangles are congruent, if they have same ______ and ______.
