Advertisements
Advertisements
प्रश्न
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
उत्तर
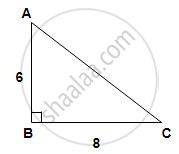
In ΔABC, ∠B = 90°, AB = 6, BC = 8
By Pythagoras theorem,
AC2 = AB2 + BC2
= 62 + 82
= 36 + 64
AC2 = 100
∴ AC = 10 units
APPEARS IN
संबंधित प्रश्न
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In the given figure. PQ = PS, P =R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Two circles having same circumference are congruent.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
