Advertisements
Advertisements
प्रश्न
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
उत्तर
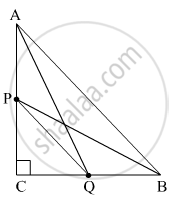
Using the Pythagoras theorem in ΔABC, ΔACQ, ΔBPC, ΔPCQ, we get
AB2 = AC2 + BC2 ......(1)
AQ2 = AC2 + CQ2 ......(2)
BP2 = PC2 + BC2 .......(3)
PQ2 = PC2 + CQ2 .......(4)
Adding the equations (2) and (3) we get
AQ2 + BP2 = AC2 + CQ2 + PC2 + BC2
= (AC2 + BC2) + (CQ + PC2)
= AB2 + PQ2
As
L.H.S. = AQ2 + BP2
= AB2 + PQ2
= R.H.S
Hence Proved
संबंधित प्रश्न
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
