Advertisements
Advertisements
प्रश्न
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
पर्याय
120 cm
122 cm
71 cm
142 cm
Advertisements
उत्तर
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is 142 cm.
Explanation:
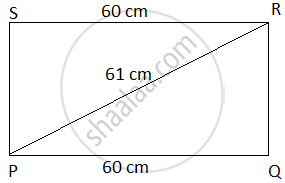
Consider the rectangle PQRS,
Given, length of rectangle PQ = 60 cm, Diagonal of the rectangle = 61 cm.
To find out the height of the rectangle, consider the right angled triangle PQR.
From the Pythagoras theorem,
PR2 = PQ2 + RQ2
⇒ 612 = 602 + RQ2
⇒ 3721 = 3600 + RQ2
⇒ RQ2 = 3721 – 3600
⇒ RQ2 = 121
⇒ RQ = `sqrt(121)`
⇒ RQ = 11 cm
Then, the perimeter of the rectangle PQRS = 2(Length + Breadth)
= 2(60 + 11)
= 2(71)
= 142 cm
APPEARS IN
संबंधित प्रश्न
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
In the figure below, find the value of 'x'.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a right angled triangle, the hypotenuse is the greatest side
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
