Advertisements
Advertisements
प्रश्न
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
विकल्प
120 cm
122 cm
71 cm
142 cm
उत्तर
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is 142 cm.
Explanation:
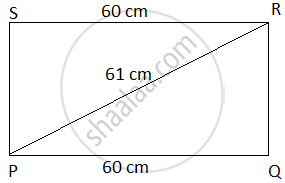
Consider the rectangle PQRS,
Given, length of rectangle PQ = 60 cm, Diagonal of the rectangle = 61 cm.
To find out the height of the rectangle, consider the right angled triangle PQR.
From the Pythagoras theorem, PR2 = PQ2 + RQ2
⇒ 612 = 602 + RQ2
⇒ 3721 = 3600 + RQ2
⇒ RQ2 = 3721 – 3600
⇒ RQ2 = 121
⇒ RQ = `sqrt(121)`
⇒ RQ = 11 cm
Then, the perimeter of the rectangle PQRS = 2(Length + Breadth)
= 2(60 + 11)
= 2(71)
= 142 cm
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
