Advertisements
Chapters
![NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 6 - Triangles NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 6 - Triangles - Shaalaa.com](/images/mathematics-english-class-7_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 6: Triangles
Below listed, you can find solutions for Chapter 6 of CBSE NCERT Exemplar for Mathematics [English] Class 7.
NCERT Exemplar solutions for Mathematics [English] Class 7 6 Triangles Exercise [Pages 159 - 185]
Four options are given, out of which only one is correct. Choose the correct one.
The sides of a triangle have lengths (in cm) 10, 6.5 and a, where a is a whole number. The minimum value that a can take is ______.
6
5
3
4
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
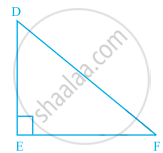
They are equal angles
They form a pair of adjacent angles
They are complementary angles
They are supplementary angles
In the given figure, PQ = PS. The value of x is ______.
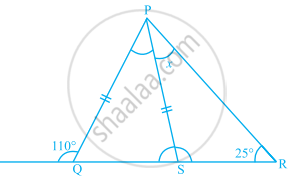
35°
45°
55°
70°
In a right-angled triangle, the angles other than the right angle are ______.
obtuse
right
acute
straight
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
(i) only
(ii) only
(iii) only
(i) and (ii)
In a triangle, one angle is of 90°. Then ______.
- The other two angles are of 45° each
- In remaining two angles, one angle is 90° and other is 45°
- Remaining two angles are complementary
In the given option(s) which is true?
(i) only
(ii) only
(iii) only
(i) and (ii)
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Obtuse angled triangle
Acute-angled triangle
Right-angled triangle
An Isosceles right triangle
In the given figure, PB = PD. The value of x is ______.
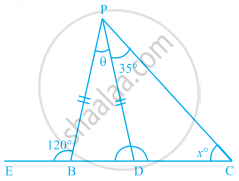
85°
90°
25°
35°
In ∆PQR, ______.
PQ – QR > PR
PQ + QR < PR
PQ – QR < PR
PQ + PR < QR
In ∆ABC ______.
AB + BC > AC
AB + BC < AC
AB + AC < BC
AC + BC < AB
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
25 m
13 m
18 m
17 m
The triangle ABC formed by AB = 5 cm, BC = 8 cm, AC = 4 cm is ______.
an isosceles triangle only
a scalene triangle only
an isosceles right triangle
scalene as well as a right triangle
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
3 m
5 m
4 m
11 m
If in an isosceles triangle, each of the base angles is 40°, then the triangle is ______.
Right-angled triangle
Acute angled triangle
Obtuse angled triangle
Isosceles right-angled triangle
If two angles of a triangle are 60° each, then the triangle is ______.
Isosceles but not equilateral
Scalene
Equilateral
Right-angled
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
120 cm
122 cm
71 cm
142 cm
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
40°
80°
120°
50°
Which of the following statements is not correct?
The sum of any two sides of a triangle is greater than the third side
A triangle can have all its angles acute
A right-angled triangle cannot be equilateral
Difference of any two sides of a triangle is greater than the third side
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
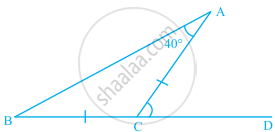
40°
80°
120°
60°
The length of two sides of a triangle are 7 cm and 9 cm. The length of the third side may lie between ______.
1 cm and 10 cm
2 cm and 8 cm
3 cm and 16 cm
1 cm and 16 cm
From the given figure, the value of x is ______.
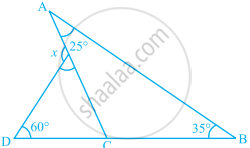
75°
90°
120°
60°
In the given figure, the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F is ______.
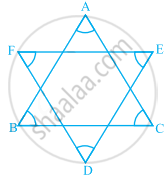
190°
540°
360°
180°
In the given figure, PQ = PR, RS = RQ and ST || QR. If the exterior angle RPU is 140°, then the measure of angle TSR is ______.
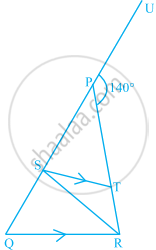
55°
40°
50°
45°
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

50°
40°
70°
60°
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
obtuse
acute
right
equilateral
If the exterior angle of a triangle is 130° and its interior opposite angles are equal, then measure of each interior opposite angle is ______.
55°
65°
50°
60°
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
70°
110°
35°
145°
In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is ______.
AD
BE
FC
DE
In ∆PQR, if ∠P = 60°, and ∠Q = 40°, then the exterior angle formed by producing QR is equal to ______.
60°
120°
100°
80°
Which of the following triplets cannot be the angles of a triangle?
67°, 51°, 62°
70°, 83°, 27°
90°, 70°, 20°
40°, 132°, 18°
Which of the following can be the length of the third side of a triangle whose two sides measure 18 cm and 14 cm?
4 cm
3 cm
5 cm
32 cm
How many altitudes does a triangle have?
1
3
6
9
If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
Median
Angle bisector
Altitude
Hypotenuse
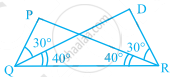
The measures of ∠x and ∠y in the given figure are respectively.
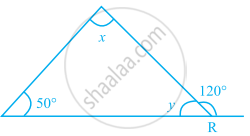
30°, 60°
40°, 40°
70°, 70°
70°, 60°
If length of two sides of a triangle are 6 cm and 10 cm, then the length of the third side can be ______.
3 cm
4 cm
2 cm
6 cm
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
3 cm
4 cm
5 cm
6 cm
In a right-angled triangle ABC, if angle B = 90°, then which of the following is true?
AB2 = BC2 + AC2
AC2 = AB2 + BC2
AB = BC + AC
AC = AB + BC
Which of the following figures will have it’s altitude outside the triangle?
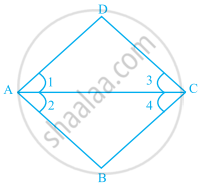
In the given figure, if AB || CD, then ______.
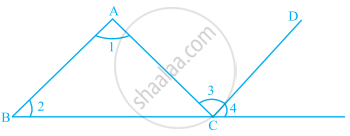
∠2 = ∠3
∠1 = ∠4
∠4 = ∠1 + ∠2
∠1 + ∠2 = ∠3 + ∠4
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
80°
20°
40°
30°
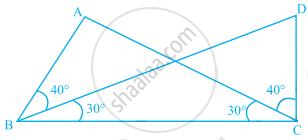
In ∆ABC, ∠Α = 50°, ∠B = 70° and bisector of ∠C meets AB in D (see figure). Measure of ∠ADC is ______.
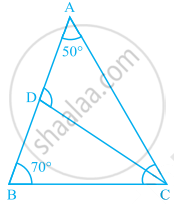
50°
100°
30°
70°
If for ∆ABC and ∆DEF, the correspondence CAB `leftrightarrow` EDF gives a congruence, then which of the following is not true?
AC = DE
AB = EF
∠A = ∠D
∠C = ∠E
In the given figure, M is the mid-point of both AC and BD. Then ______.
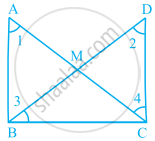
∠1 = ∠2
∠1 = ∠4
∠2 = ∠4
∠1 = ∠3
If D is the mid-point of the side BC in ∆ABC where AB = AC, then ∠ADC is ______.
60°
45°
120s°
90°
Two triangles are congruent, if two angles and the side included between them in one of the triangles are equal to the two angles and the side included between them of the other triangle. This is known as the ______.
RHS congruence criterion
ASA congruence criterion
SAS congruence criterion
AAA congruence criterion
By which congruency criterion, the two triangles in the given figure are congruent?
RHS
ASA
SSS
SAS
By which of the following criterion two triangles cannot be proved congruent?
AAA
SSS
SAS
ASA
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?
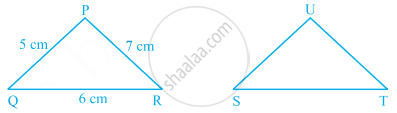
5 cm
6 cm
7 cm
cannot be determined
If ∆ABC and ∆DBC are on the same base BC, AB = DC and AC = DB (see figure), then which of the following gives a congruence relationship?
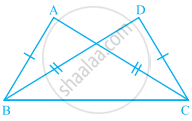
∆ABC ≅ ∆DBC
∆ABC ≅ ∆CBD
∆ABC ≅ ∆DCB
∆ABC ≅ ∆BCD
Fill in the blanks to make the statements true.
The ______ triangle always has altitude outside itself.
The sum of an exterior angle of a triangle and its adjacent angle is always ______.
The longest side of a right angled triangle is called its ______.
Median is also called ______ in an equilateral triangle.
Measures of each of the angles of an equilateral triangle is ______.
In an isosceles triangle, two angles are always ______.
In an isosceles triangle, angles opposite to equal sides are ______.
If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
Every triangle has at least ________ acute angles
Two line segments are congruent, if they are of ______ lengths.
Two angles are said to be ______, if they have equal measures.
Two rectangles are congruent, if they have same ______ and ______.
Two squares are congruent, if they have same ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠R = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QR = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠P = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QP = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠Q = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then RP = ______.
In the given figure, ∆PQR ≅ ∆ ______.
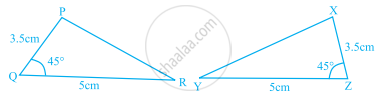
In the given figure, ΔPQR ≅ Δ ______.
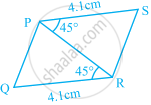
In the given figure, Δ______ ≅ ΔPQR.
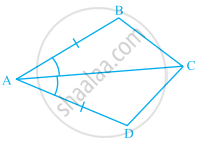
In the given figure, ∆ARO ≅ ∆______.
In the given figure, AB = AD and ∠BAC = ∠DAC. Then
- ∆ ______ ≅ ∆ABC.
- BC = ______.
- ∠BCA = ______.
- Line segment AC bisects ______ and ______.
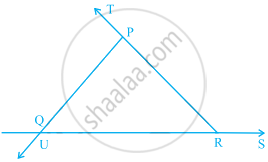
In the given figure, ∠TPQ = ∠ _____ + ∠ _____
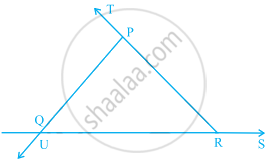
In the given figure, ∠UQR = ∠______ + ∠ ______
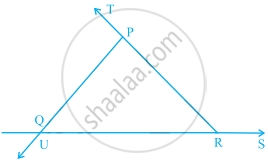
In the given figure, ∠PRS = ∠ ______ + ∠ _______
State whether the statements are True or False.
In a triangle, sum of squares of two sides is equal to the square of the third side.
True
False
Sum of two sides of a triangle is greater than or equal to the third side.
True
False
The difference between the lengths of any two sides of a triangle is smaller than the length of third side.
True
False
In ∆ABC, AB = 3.5 cm, AC = 5 cm, BC = 6 cm and in ∆PQR, PR = 3.5 cm, PQ = 5 cm, RQ = 6 cm. Then ∆ABC ≅ ∆PQR.
True
False
Sum of any two angles of a triangle is always greater than the third angle.
True
False
The sum of the measures of three angles of a triangle is greater than 180°.
True
False
It is possible to have a right-angled equilateral triangle.
True
False
If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent.
True
False
It is possible to have a triangle in which two of the angles are right angles.
True
False
It is possible to have a triangle in which two of the angles are obtuse.
True
False
It is possible to have a triangle in which two angles are acute.
True
False
It is possible to have a triangle in which each angle is less than 60°.
True
False
It is possible to have a triangle in which each angle is greater than 60°.
True
False
It is possible to have a triangle in which each angle is equal to 60°.
True
False
A right-angled triangle may have all sides equal.
True
False
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
True
False
In the given figures, two triangles are congruent by RHS.
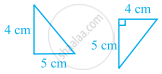
True
False
The congruent figures super impose each other completely.
True
False
A one rupee coin is congruent to a five rupee coin.
True
False
The top and bottom faces of a kaleidoscope are congruent.
True
False
Two acute angles are congruent.
True
False
Two right angles are congruent.
True
False
Two figures are congruent, if they have the same shape.
True
False
If the areas of two squares is same, they are congruent.
True
False
If the areas of two rectangles are same, they are congruent.
True
False
If the areas of two circles are the same, they are congruent.
True
False
Two squares having same perimeter are congruent.
True
False
Two circles having same circumference are congruent.
True
False
If three angles of two triangles are equal, triangles are congruent.
True
False
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
True
False
If two sides and one angle of a triangle are equal to the two sides and angle of another triangle, then the two triangles are congruent.
True
False
If two triangles are congruent, then the corresponding angles are equal.
True
False
If two angles and a side of a triangle are equal to two angles and a side of another triangle, then the triangles are congruent.
True
False
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
True
False
If hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent.
True
False
AAS congruence criterion is same as ASA congruence criterion.
True
False
In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then, ∆ABD ≅ ∆ACD by RHS.
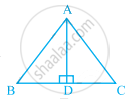
True
False
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
In the given figure, find the value of x.
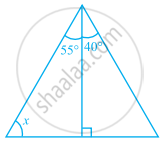
In the given figure, find the values of a, b and c.
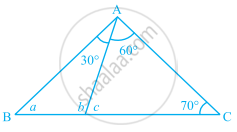
In the given figure, find the values of a, b and c
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
I have three sides. One of my angle measures 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
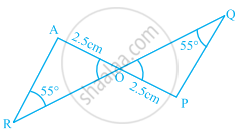
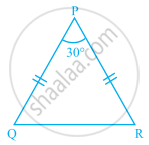
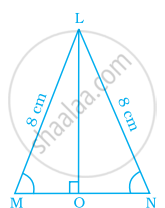
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
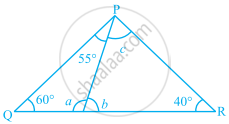
In the given figure, find the measures of ∠x and ∠y.
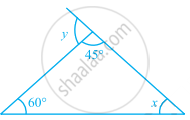
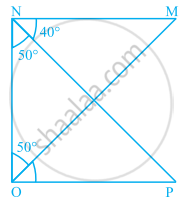
In the given figure, find the measures of ∠PON and ∠NPO.
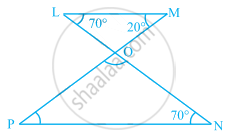
In the given figure QP || RT. Find the values of x and y.
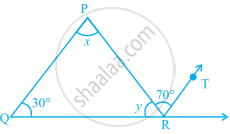
Find the measure of ∠A in the given figure.
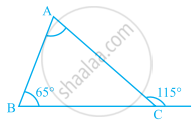
In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is 360°.
In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
Find the values of x and y in the given figure.
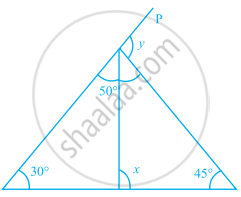
Find the value of x in the given figure.

The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
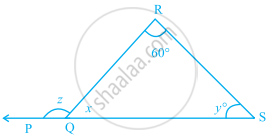
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

In the given figure, find the values of x, y and z.
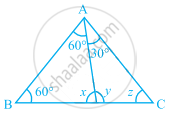
If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
In the given figure, ∆PQR is right-angled at P. U and T are the points on line QRF. If OP || ST and US || RP, find ∠S.

In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
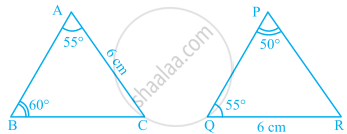
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
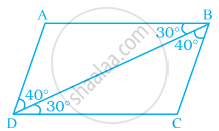
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
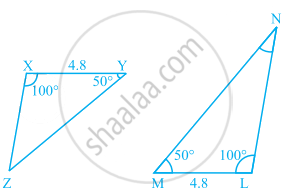
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
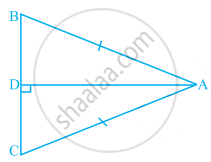
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:

In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
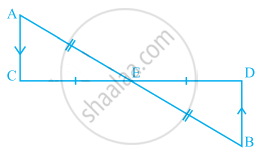
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
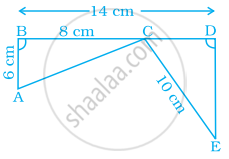
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
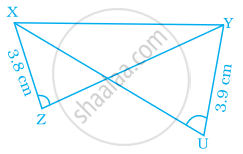
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
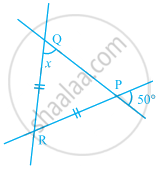
In the given figure, if RP = RQ, find the value of x.
In the given figure, if ST = SU, then find the values of x and y.

Check whether the following measures (in cm) can be the sides of a right-angled triangle or not.
1.5, 3.6, 3.9
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
In the given figure, if y is five times x, find the value of z.
The lengths of two sides of an isosceles triangle are 9 cm and 20 cm. What is the perimeter of the triangle? Give reason.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
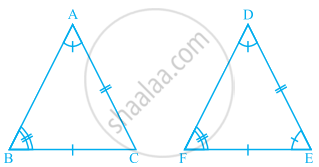
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
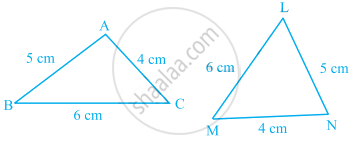
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.

In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
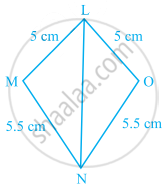
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
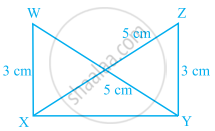
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
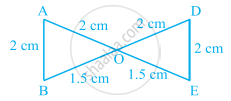
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.

In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
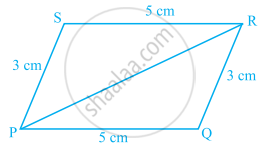
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
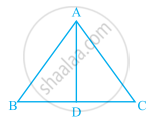
ABC is an isosceles triangle with AB = AC and D is the mid-point of base BC (see figure).
- State three pairs of equal parts in the triangles ABD and ACD.
- Is ∆ABD ≅ ∆ACD. If so why?
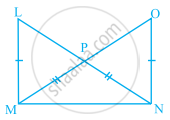
In the given figure, it is given that LM = ON and NL = MO
- State the three pairs of equal parts in the triangles NOM and MLN.
- Is ∆NOM ≅ ∆MLN. Give reason?
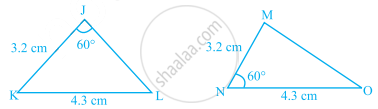
Triangles DEF and LMN are both isosceles with DE = DF and LM = LN, respectively. If DE = LM and EF = MN, then, are the two triangles congruent? Which condition do you use? If ∠E = 40°, what is the measure of ∠N?
If ΔPQR and ΔSOR are both isosceles triangle on a common base OR such that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent? Which condition do you use?
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
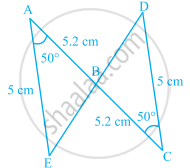
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
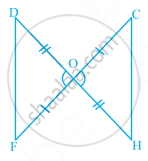
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
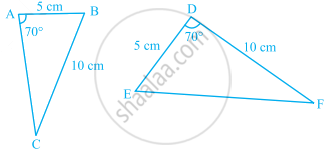
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
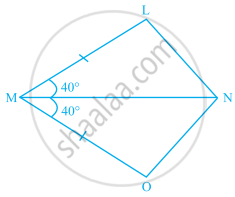
State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
∆PQR: PQ = 3.5 cm, QR = 4.0 cm, ∠Q = 60°
∆STU: ST = 3.5 cm, TU = 4 cm, ∠T = 60°
State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
∆ABC: AB = 4.8 cm, ∠A = 90°, AC = 6.8 cm
∆XYZ: YZ = 6.8 cm, ∠X = 90°, ZX = 4.8 cm
In the given figure, PO = PS and ∠1 = ∠2.
- Is ∆PQR ≅ ∆PSR? Give reasons.
- Is QR = SR? Give reasons.
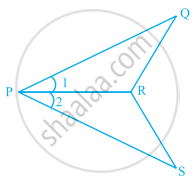
In the given figure, DE = IH, EG = FI and ∠E = ∠I. Is ∆DEF ≅ ∆HIG? If yes, by which congruence criterion?
In the given figure, ∠1 = ∠2 and ∠3 = ∠4.
- Is ∆ADC ≅ ∆ABC? Why ?
- Show that AD = AB and CD = CB.
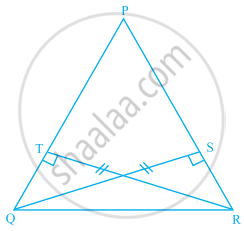
Observe the given figure and state the three pairs of equal parts in triangles ABC and DBC.
- Is ∆ABC ≅ ∆DCB? Why?
- Is AB = DC? Why?
- Is AC = DB? Why?
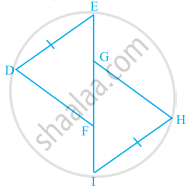
In the given figure, QS ⊥ PR, RT ⊥ PQ and QS = RT.
- Is ∆QSR = ∆RTO? Give reasons.
- Is ∠PQR = ∠PRQ? Give reasons.
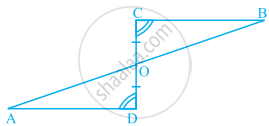
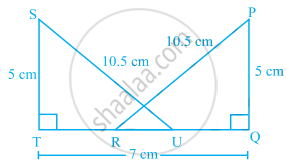
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
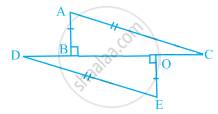
In the given figure, state the three pairs of equal parts in ΔABC and ΔEOD. Is ΔABC = ΔEOD? Why?
Solutions for 6: Triangles
![NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 6 - Triangles NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 6 - Triangles - Shaalaa.com](/images/mathematics-english-class-7_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 6 - Triangles
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 7 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 7 CBSE 6 (Triangles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 7 chapter 6 Triangles are Concept of Triangles, Median of a Triangle, Classification of Triangles (On the Basis of Sides, and of Angles), Altitudes of a Triangle, Exterior Angle of a Triangle and Its Property, Angle Sum Property of a Triangle, Sum of the Lengths of Two Sides of a Triangle, Right-angled Triangles and Pythagoras Property, Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene, Some Special Types of Triangles - Equilateral and Isosceles Triangles, Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene, Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled, Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled, Congruence of Plane Figures, Congruence Among Line Segments, Congruence of Angles, Congruence of Triangles, Criteria for Congruence of Triangles, RHS Congruence Criterion, SSS Congruence Criterion, SAS Congruence Criterion, ASA Congruence Criterion, Exceptional Criteria for Congruence of Triangles.
Using NCERT Exemplar Mathematics [English] Class 7 solutions Triangles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 7 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 6, Triangles Mathematics [English] Class 7 additional questions for Mathematics Mathematics [English] Class 7 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.