Advertisements
Advertisements
प्रश्न
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
उत्तर
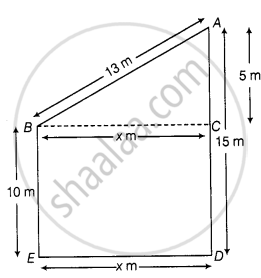
Let BC = x m
In right-angled ΔACB,
AB2 = AC2 + BC2 ......[By Pythagoras theorem]
⇒ (13)2 = (5)2 + x2
⇒ 169 – 25 = x2
⇒ 144 = x2
⇒ x = `sqrt(144)`
⇒ x = 12 m
Hence, the distance between the feet of two poles is 12 m.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
